Sorting and its types

Sorting

• Sorting refers to the operation or technique of arranging and rearranging sets of data in some specific order. 
  
• There are basically two types of as per location or memory.
• Internal Sorting: 
• If all the items need to be sorted are in main memory or RAM such an algorithm of sorting called Internal Sorting..
• External Sorting:
• If all the items need to be sorted are not in main memory or RAM or need the help of other external memory such an algorithm of sorting called External Sorting.

• There are basically two types of as per order:
• The data are either sorted either numerically or alphanumerically
• For example "SARTHAK" => in Ascending, AAHKRST and in Descending, TSRKHAA
• For Example 10,30,20 in Ascending, 10,20,30 and in Descending, 30,20,10
• The comparison operator is used to decide the new order of the element in the respective data structure.
• Ascending (Lower to Higher)
• Descending (Higher to Lower)
  

Categories of Sorting

• Bubble Sort
  
• Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order.
• This algorithm is suitable for small data sets
• Its average and worst-case complexity are of (n^2) where n is the number of items.
• It is known as bubble sort because with every complete iteration the largest element bubbles up towards the last place or the highest index just like a water bubble rises up to the water surface.
• Algorithm:

bubbleSort(array)
  for i <- span=""> 1 to indexOfLastUnsortedElement-1
    if leftElement > rightElement
      swap leftElement and rightElement
end bubbleSort

• Insertion Sort
  
• Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands.
• Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time.
• Efficient for (quite) small data sets.
• Algorithm:

selectionSort(array, size)
  repeat (size - 1) times
  set the first unsorted element as the minimum
  for each of the unsorted elements
    if element < currentMinimum
      set element as new minimum
  swap minimum with first unsorted position
end selectionSort

• Selection Sort
  
• Selection sort is a sorting algorithm, specifically an in-place comparison sort.
• It is inefficient on large lists.
• The algorithm divides the input list into two parts: the sublist of items already sorted, which is built up from left to right at the front (left) of the list, and the sublist of items remaining to be sorted that occupy the rest of the list.
• Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. 
• The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
• Quick Sort
  
• Quick Sort Algorithm is a Divide & Conquer algorithm. 
• It divides input array into two partitions, calls itself for the two partitions(recursively) and performs in-place sorting while doing so. 
• A separate partition() function is used for performing this in-place sorting at every iteration. 
• Quicksort is one of the most efficient sorting algorithms.
• Algorithm –
• There are 2 Phases (3 major steps) in the Quick Sort Algorithm –
• Division Phase – Divide the array(list) into 2 halves by finding the pivot point to perform the partition of the array(list).
• The in-place sorting happens in this partition process itself.
• Recursion Phase –
• Call Quick Sort on the left partition (sub-list)
• Call Quick Sort on the right partition (sub-list)

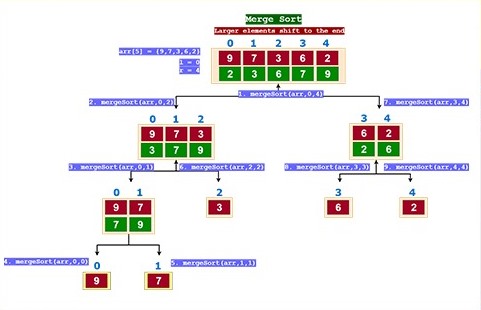
• Merge Sort
  
• Merge Sort Algorithm is a Divide & Conquer algorithm. 
• It divides input array in two halves, calls itself for the two halves(recursively) and then merges the two sorted halves. 
• A separate merge() function is used for merging two halves. 
• Merge sort is one of the most efficient sorting algorithms.
• Algorithm–
• There are 3 Phases (4 major steps) in the Merge Sort Algorithm –
• Division Phase – Divide the array(list) into 2 halves by finding the midpoint of the array(list).
• Midpoint (m) = (left + right)/ 2
• Here left is the starting index & right is the last index of the array(list)
• Recursion Phase –
• Call Merge Sort on the left sub-array (sub-list)
• Call Merge Sort on the right sub-array (sub-list)
• Merge Phase –
• Call merge function to merge the divided sub-arrays back to the original array.
• Perform sorting of these smaller sub arrays before merging them back.
• Radix Sort
• Radix sort is a non-comparative sorting algorithm. 
• It avoids comparison by creating and distributing elements into buckets according to their radix. 
• For elements with more than one significant digit, this bucketing process is repeated for each digit, while preserving the ordering of the prior step, until all digits have been considered. 
• For this reason, radix sort has also been called bucket sort and digital sort. Typically Radix sort uses counting sort as a subroutine to sort. 
• Algorithm –
• Step 1 – Take input array and find MAX number in the array
• Step 2 – Define 10 queues each representing a bucket for each digit from 0 to 9.
• Step 3 – Consider the least significant digit of each number in the list which is to be sorted.
• Step 4 – Insert each number into their respective queue based on the least significant digit.
• Step 5 – Group all the numbers from queue 0 to queue 9 in the order they have inserted into their respective queues.
• Step 6 – Repeat from step 3 based on the next least significant digit.
• Step 7 – Repeat from step 2 until all the numbers are grouped based on the most significant digit.
• Shell Sort
  
• shell sort is an in-place comparison sort.  
• It is mainly a variation of sorting by exchange (bubble sort) or sorting by insertion (insertion sort). 
• This algorithm avoids large shifts as in case of insertion sort if the smaller value is to the far right and has to be moved to the far left. 
• The idea of shell sort is to allow exchange of far items. 
• This spacing is termed as interval or gap. 
• shell sort is more efficient compared to Insertion Sort or Bubble sort especially when –
• 1. Smaller value elements are towards the end of the array/list
• 2. Large-sized array/list
• 3. Efficiency depends on how we select the GAP/interval
• Algorithm:
• Step 1 − Initialize the value of gap/interval (here we take n/2 iteratively)
• Step 2 − Compare 2 elements at the distance of gap at every iteration
• Step 3 − if the element at the left is smaller than the element at the right, perform swap or shift(depending on whether you use bubble sort or insertion sort respectively)
• Step 4 − Repeat until the complete list is sorted.